GNN

应用领域

图可以标识事物之间的相关关系，图在场景分析问题推理、推荐系统、风控 甚至无人汽车等多方面都有很大作用。

基本组成

点：是特征，由特征向量表示

边：表示点之间的关系，也有特征。所有的边类型相同

图：全局的图，是向量

输入时要输入点的特征和邻接矩阵，邻接矩阵表示关系。

优势

传统神经网络输入的规模固定（比如CNN输入图像一般都是256或512），在实际应用时，分子结构、或交通道路等点和边个数不同，难以使用传统的神经网络（resize强行改成相同效果可能不好）

GNN优势就是处理不规则数据

实际输入的邻接矩阵一般不是N*N的，而是2*N，即source->target

训练

在对点进行更新的时候，不仅要考虑自身的信息，还要考虑邻接的信息。

如上图，在更新6的时候要考虑1，3，4的信息。以1为例，1要给6多少信息取决于可学习的权重参数w1和1本身的特征x1

聚合：每个点提供的特征是由可学习的参数经过特征映射得到的结果：$$\bar{a_i}=G({W_j \cdot x_j:j \in N_i})$$

最后将信息进行汇总：

$$h_i=\sigma(W_1 \cdot h_i+\sum_{j \in N_i} \mathbf{W}_2 \cdot h_j)$$

前面表示自己的特征 后面表示邻居的特征，类似于加权。

邻接与当前点的关系有很多可选的方式：

输入矩阵不变，只更新点的特征。虽然每个点相邻的点不变，但是在不断更新中，可以得到与其他未连接点的关系，感受野不断变大。

输出的特征可用于分类、回归等。

GCN

GCN与CNN差别较大：输入方面

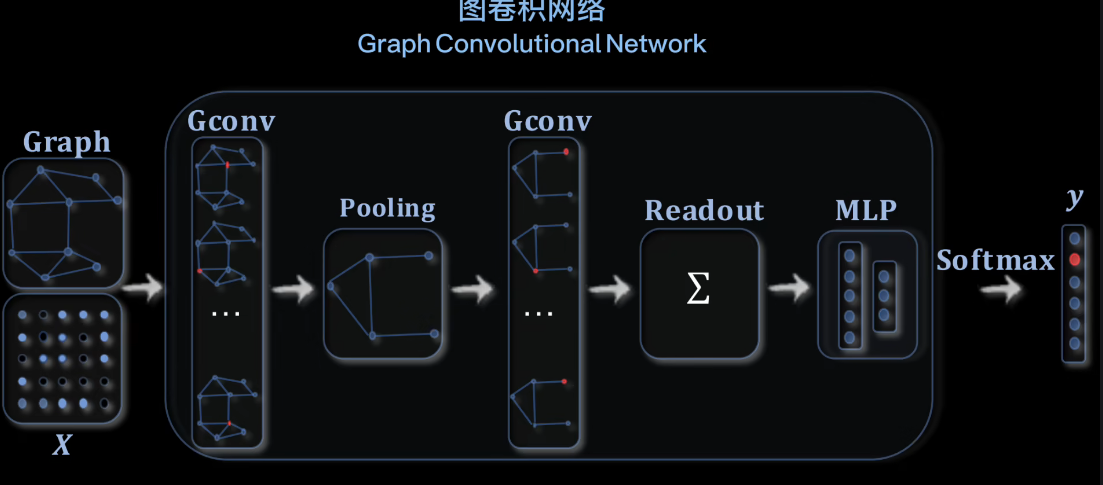
优势

不需要全部都有标签，少量标签也可以训练，计算损失只用有标签的。适合半监督任务